正五角形の作図法

正五角形の一辺の長さ

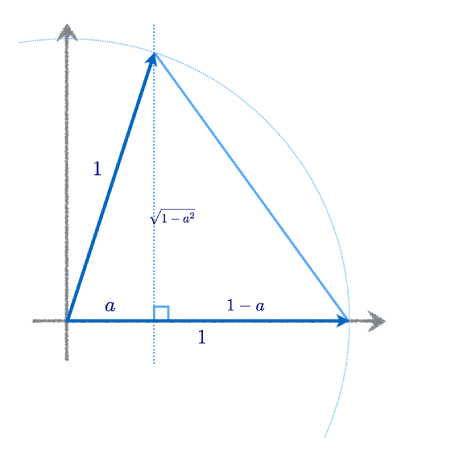
ここでは、半径１の円に内接する正五角形の一辺の長さを計算して、正五角形の作図方法を説明します。正五角形の内角は $2\pi/5$ ラジアン（72°）であることから、まず最初に $a = \cos(2\pi/5)$ を使って一辺の長さを計算します。

右の図に従って３平方の定理を２回利用すると、正五角形の一辺の長さは $\sqrt{(1-a)^2 + (\sqrt{1-a^2})^2} = \sqrt{1-2a+a^2 + 1 -a^2} = \sqrt{2-2a}$ となることが導かれます。

$\cos(2\pi/5)$ の計算

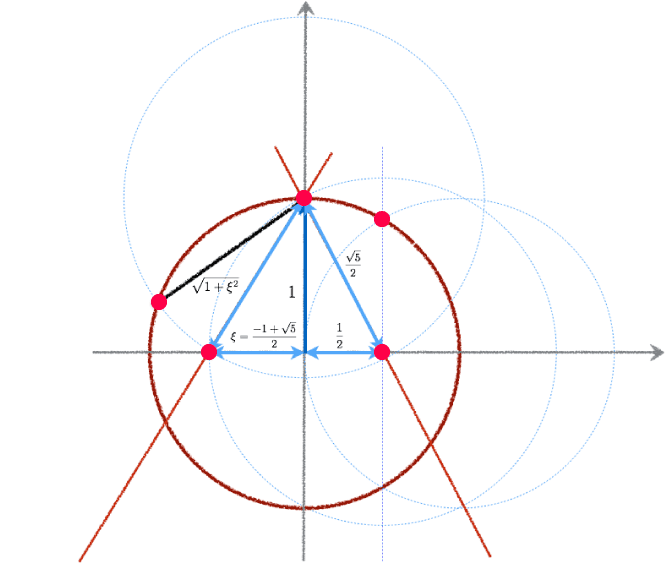
次に $\cos(2\pi/5)$ の値を求めます。複素数 $\zeta_5 = \cos(2\pi/5) + i \sin(2\pi/5)$ は $5$ 乗すると $1$ になることから、 $f(X) = X^5-1 = 0$ の解となります。 $f(X) = (X-1)(X^4+X^3+X^2+X+1) = 0$ であり、 $\zeta_5\neq 1$ であることから、 $\zeta_5^4+\zeta_5^3+\zeta_5^2+\zeta_5+1=0$ が導かれます。いま、 $\zeta^4_5 = \cos(8\pi/5) + i \sin(8\pi/5) = \cos(2\pi/5) – i \sin(2\pi/5)$ が成り立つことから、 $\zeta_5 + \zeta^4_5 = 2\cos(2\pi/5)$ が導かれます。 $\xi = \zeta_5 + \zeta^4_5$ , $\xi’ = \zeta^2_5 + \zeta^3_5$ と置くと、 $\begin{align} \xi+\xi’ &= (\zeta_5 + \zeta^4_5) + (\zeta^2_5 + \zeta^3_5) = \zeta_5^4+\zeta_5^3+\zeta_5^2+\zeta_5 =-1 \\ \xi\xi’ &= (\zeta_5 + \zeta^4_5) (\zeta^2_5 + \zeta^3_5) = \zeta_5^3+\zeta_5^4+\zeta_5^6+\zeta_5^7= \zeta_5^4+\zeta_5^3+\zeta_5^2+\zeta_5 =-1 \end{align}$ となります。

二次方程式の解と係数の関係から、 $\xi, \xi’$ は二次方程式 $g(x) = x^2 + x – 1 = 0$ の解となります。従って、二次方程式の解の公式と $\xi =2\cos(2\pi/5)>0$ が成り立つことより $\xi = \frac{-1 +\sqrt{5}}{2}$ が導かれます。以上の計算から、半径１の円に内接する正五角形の一辺の長さは $\xi^2+\xi-1=0$ に注意すると $\sqrt{2-2a} = \sqrt{2-\xi} = \sqrt{1 + (1-\xi)} = \sqrt{1 + \xi^2}$ となります。作図をするためにはこの計算で十分ですが、数値を具体的に求めると $\sqrt{1+\xi^2} =\sqrt{ \frac{4+(6 -2\sqrt{5})}{4}} = \frac{\sqrt{10-2\sqrt{5}}}{2}$ となります。