博士論文とは、大学卒業後、大学院の修士課程を修了し、さらに博士課程へ進んで研究した内容をまとめたものです。難しい言葉もたくさんあります。わからないことだらけでも全く大丈夫！！研究の雰囲気や、数学の世界にどんな分野やテーマがあるのか感じてもらえればと思います。研究者同士でも、お互いの博士論文の内容はなかなか理解できるものではありません。実はわからないことって面白いことの始まりです。存分に楽しんでください♪

論文題目「Solvability for the mathematical model representing motions of the elastic curves on the plane」
（日本女子大学にて取得。）

I.博士論文の内容と扱った問題

　私の博士論文のテーマは、弾性閉曲線の伸縮運動を表す微分方程式モデルの構築とその数学解析です。博士課程前期の頃、「形状記憶合金におけるヒステリシスの原理は完全には解明されていない」ことを知りました。弾性体の一種である形状記憶合金では、物体の状態変化が温度に依存することが知られています。いま、手元に真っ直ぐな形状記憶合金の針金があって力を加えて変形したとしましょう。アルミなどの金属でできた針金であれば、金属の温度に依らず変形したままの状態を保ちます。しかし、形状記憶合金の場合、ある一定の温度以上になると、元の状態に戻る、つまり、真っ直ぐになる、という現象が起こります。この「形状記憶効果」にはヒステリシスという物理現象が関係していますが、その原理を完全に表した数理モデルはありません。この現象の解明に貢献できるよう、研究の初期段階として「弾性体の物理的性質を数学的に表現すること」を目標にしました。具体的には、研究課題として、次の初期値境界値問題による「平面上の弾性閉曲線の伸縮運動の定式化」に取り組みました。

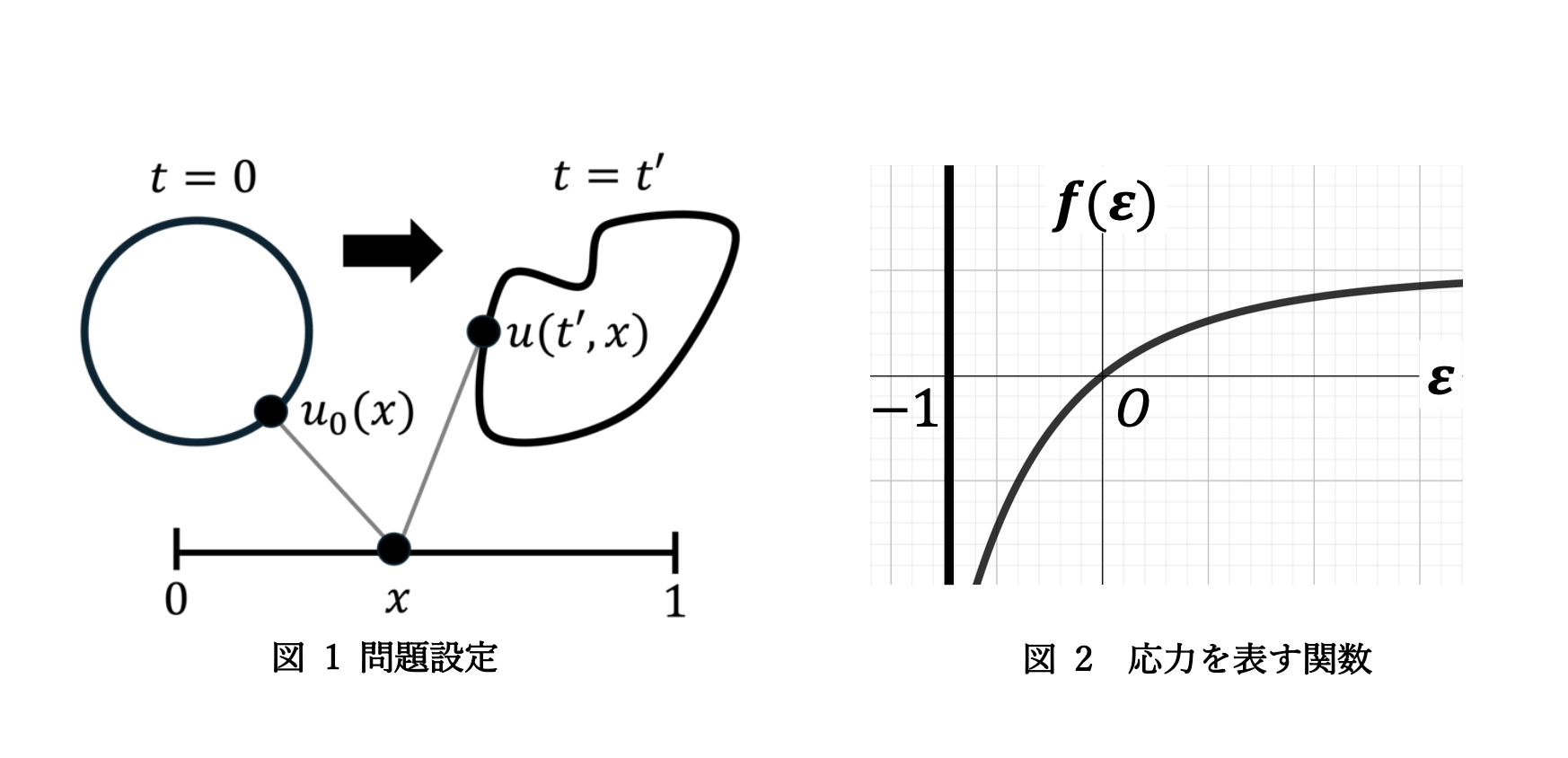
　この問題では、図 1 のように、自然長を 1 とする弾性体の両端点をつなぎ合わせて平面上の閉曲線とみなし、その伸縮運動を考えます。未知関数 \(u\) は \((0, T) \times (0, 1)\)（ただし、 \(T > 0\)）から \(\mathbb{R}^2\) へのベクトル値関数で、時刻 \(t \in (0, T)\) における弾性体の平面上の位置を表します。\(\rho > 0\) は弾性体の密度を表す定数、\(\gamma > 0\), \(\mu \ge 0\) は定数です。\( \varepsilon \) は歪みを表し、この問題では \( \varepsilon = \lvert \partial_x u \rvert  – 1 \) で定義します。これは、未知関数が平面上の位置を表すことと歪みの定義に由来します。この問題では、歪みは長さの変化率で定義され、\( -1 \) 以上の値を取ることがすぐ分かります。\( f \) は \( (-1,\infty) \)から \( \mathbb{R} \) への関数で、応力を表し、次を仮定します。

　ここで、\( \kappa > 0 \)は定数です。この \( f \) は、図2のように \( \varepsilon \to -1 \) のとき \( f(\varepsilon) \to -\infty \) になることが分かります。これは「弾性閉曲線を 1 点に潰すと、生じる応力が極めて大きくなる」ことを数学的に表しています。このような「特異性をもつ関数で応力を表現」している点が本研究の特徴の 1 つです。境界条件は周期境界条件を課します。この条件は、弾性体の繋ぎ目が滑らかな状態であることを意味します。最後に、\( u_0 \) は弾性体の初期位置、\( v_0 \) は弾性体の初速度を表します。

　博士論文では、まず、弾性閉曲線の伸縮運動を表す方程式として、エネルギー保存則から上述の方程式を導出しました。そして、この初期値境界値問題を平面上の弾性閉曲線の伸縮運動を表す微分方程式モデルとして定式化するために、その数学的適切性を考察しました。より具体的には、この問題の解の存在や一意性を数学的に示しました。 その際、 従来のモデルでは得られていない「歪みが \(-1\) より大きくなることを保証する良い評価」を解の性質として得ることができました。一方、このモデルの構築では、現象を簡略化し「弾性体の大きな動きも表現できる応力の数学的表現として特異性をもつ関数を定式化」することに焦点を当てていました。そのことから次の研究段階として、重力や曲率も考慮したモデルの考察が課題として挙げられます。

II.今後の展望

　博士論文で扱った弾性閉曲線の伸縮運動を表す微分方程式モデルを発展させて、形状記憶合金の針金の輪の回転運動を表すモデルを構築することです。そして、モデルの数学的・数値解析的考察が、形状記憶合金の変形や移動の原理解明への一助となるよう、今後も研究に励みます。

※2026年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。