私が数学の便利さを痛感するようになったのは、大学院でコンピュータビジョンという学問に出会ってからです。コンピュータビジョンは、計算機で人間の視覚を実現する、という、どうやって取り組んでよいか見当も付かない問題を扱う分野です。与えられた画像や動画の中から文字を読み取ったり、写っている人の顔を判別したり、そもそも何が写っているかを判断したりと、幅広い応用があります。ここで、数学は世界や問題を抽象化し普遍的に記述できる素晴らしい力を発揮します。

ベクトルについて

皆さんは、もうベクトルについて勉強しているでしょうか？私が初めて高校の数学や物理で習ったときは、「長さと方向を持つもの」、というように教えられて、即座には理解できなかったことを覚えています。今、私は、もう少し違う見方をしています。ベクトルは、「数値の組」、あるいは、「数値を拡張したもの」、と理解しています。

数値の拡張がどのように便利なのでしょうか？そもそも「ベクトル」とは何でしょうか？ベクトルは、「数値」を並べたものです。$[3.5, 1.0, 2.0]$　、あるいは、$[6.0, 5.9, 3.7, 4.0, 8.1, 2.5, 9.4]$ のように書いたりします。前者は数字が三つ並んでいるので、三次元ベクトル^*1、後者は七次元ベクトルです。数字を追加すれば、次元は自由に増やせます^*2。縦に並べたり横に並べたりできますが、今はあまり気にせずに横に長いベクトルを考えていきましょう。

ベクトルはなぜ便利なのか？それは多次元の量が一つに表せるからです。多次元の量にはどんなものがあるでしょうか^*1？（例は何でも良いのですが、私は画像を扱っているので、）一つには画像があります。画像をベクトルで表すと、コンピュータに画像を認識させるといった演算が簡単に表現できます。では、ほんの初歩だけですが、実際にどのようにやるのか見てみましょう。

図１　手書きの数字の画像MNIST [1]より

たとえば右の図１のような色々な手書きの数字の画像があったとします。これを、まずは、ベクトルにしてみます。例として、図１の一番左にある「２」という数字を、図２のような数値の羅列で表します。28×28のマス目に、明るさを表す数値が入っています。0は真っ黒で、255が一番明るい白を表しています^*4。

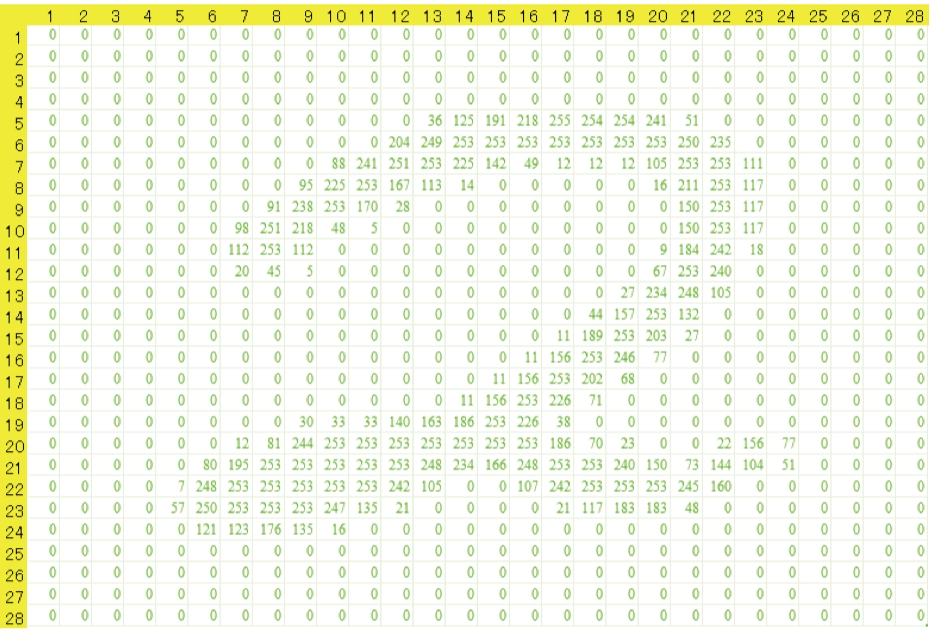
図２　２という画像（図１の一番左）を明るさの数値で表したもの

図２をベクトル化するやり方の一つ

図２を一列の長いベクトル（数値の羅列）で表してみましょう。やり方は色々とあります。一つのやり方としては、図３のように、

図３

上の行から順番に左から右にスキャンしていって、一つの非常に長い横長のベクトルを作ることができます^*3。このベクトルは、28×28=784次元になります。最初はずっとゼロが入っていて、125番目に36という明るさが出てきます。その次には125, 191, … と続きます。 図１の残りの「５」「７」「８」「２」という画像からも同じルールで、784次元のベクトルを作ることができます。大事なことは、他の画像にも「同じ」ルールを適用して、ベクトルを作ることです。では、これらのベクトルから何ができるのでしょうか。

内積について

ベクトルのとても便利な概念の一つに、「内積」があります。私が高校生の時、内積は２つのベクトルの角度を表すものだと教わりました $(\boldsymbol{\vec{a}}\cdot \boldsymbol{\vec{b}}=|\boldsymbol{\vec{a}}||\boldsymbol{\vec{b}}|\cos\theta)$。もし、あなたが中学生で、$\cos\theta$ が分からなくても大丈夫です。内積には別の計算方法があって、中学生でも理解できます。$\boldsymbol{\vec{a}}$ というベクトルが $[a_1, a_2, a_3, a_4, a_5]$という5次元のベクトル、$\boldsymbol{\vec{b}}$が、$[b_1, b_2, b_3, b_4, b_5]$ という5次元のベクトルだとします。そうすると、内積は、$$\boldsymbol{\vec{a}}\cdot\boldsymbol{\vec{b}}=a_1 b_1+a_2 b_2 + a_3 b_3 + a_4 b_4 + a_5 b_5$$として計算します。要素同士をかけて全部足すのです^*5。それから、ベクトルの大きさは、$$|\boldsymbol{\vec{a}}|=\sqrt{a_1^2 + a_2^2 + a_3^2 + a_4^2 + a_5^2}$$と計算します^*6。大きさをベクトルの「長さ」と言ったりもします。ベクトルの各要素を、大きさで割り算することで、ベクトルの大きさを $1$ にすることができます。

以上の内積の定義は、幾何的な理解に役立つのですが、私は今では内積を、$\boldsymbol{a}$ というベクトルと、$\boldsymbol{b}$ というベクトルがどれくらい似ているか、どれくらい共通部分があるか、を表す、と理解しています。$\boldsymbol{\vec{a}}$ と $\boldsymbol{\vec{b}}$ のベクトルの大きさが $1$ のときには^*7、ベクトルが似ているほど内積は $1$ に近くなり、似ている部分が全然無いとき、（直交している、といいます）、内積は $0$ になるのです。

それでは、内積の例を見てみましょう。たとえば、$[1, 0]$ というベクトルと、$[0, 1]$ というベクトルがあるとします。$[1, 0]$ は、横に$1$進んで上に $0$ 進む、$[0, 1]$ は、横に$0$進んで上に$1$進む、というものだとしましょう。図４の左の図が分かりやすいでしょうか。それぞれのベクトルの大きさは$1$です。要素同士の積を足して、$[1, 0]$と$[0, 1]$ の内積を計算してみましょう。$1\times 0 + 0\times 1 = 0$になりますね。一方、同じベクトル、$[1, 0]$ と、$[1, 0]$ の内積は、$1\times 1 + 0\times 0 = 1$ですし、$[0, 1]$ と $[0, 1]$ の内積も$1$になります。同じベクトルだと$1$、直交していると$0$になっているでしょう。

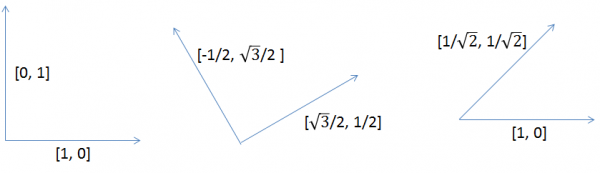
図４　二次元のベクトルの例

図１の「２」「５」「７」「８」「２」を表した784次元のベクトルに内積を適用してみましょう。ただし、それぞれのベクトルの大きさが $1$ になるようにしてから内積を計算します^*8。図１の「２」を基準にして、残りの「５」「７」「８」「２」との内積を計算すると、それぞれ、0.40、0.3、0.29、0.63、となりました。

内積はベクトルがどれくらい似ているかを表していて、似ていればいるほど $1$ に近づき、似ていなければ $0$ に近いわけですから、感覚的に理解しやすいですね。最初の「２」と最後の「２」は一番似ているので、一番内積が高くなりました。「５」「７」「８」の中で最初の「２」に似ているのは、内積が一番高い「５」と数学が教えてくれました。最初の「２」と「５」の画像を重ねてみると、重なっている部分が多いからです。

数学とその応用

数学のすごいところは、上に示したような計算が正しいことを常に保証してくれるところです。私たちは、数値が、1兆、あるいは、$0.0000001$以下の時でも、100万次元の時でも2次元の時でも、何ら心配することなく、同じ計算をして、それが正しいと確信することができます。

　でも、上の内積計算だけだと、なんだか足りなそうなところもありましたね。図１の最初の「２」と最後の「２」は、私たちには同じものに見えますが、内積は0.63で、思ったよりも高くなかった、と感じた人もいるのではないでしょうか。あるいは、「２」と「７」の方が形は似ているように見えるのに、と思った人もいるでしょう。

もう少し例を見てみましょう。たとえば、図５の上の段に示したような「２」という画像があります。下の段の「２」「５」「８」「２」と、内積をとってみた数値が、下の段のそれぞれの画像の下に書いてあります。確かに、他の「７」や「８」と比べると、「２」の画像で内積が高くなっています。ですが、内積は大体0.4くらい（角度のイメージだと、65°くらい）ですし、最初の「２」よりも、「５」の方が内積が高くなっています。（なぜそのようになるのか？考えてみて下さいね。）

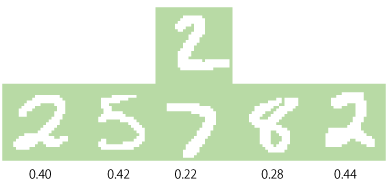
図５　別の「２」という画像（上段）と、図１の画像（下段）

どうやったら、図５の上の段にある「２」と、下の段の「２」が同じもので、「５」や「７」や「８」は違うもの、と理解させたらいいのでしょうか。そこには数学を応用した、工学や情報学の出番があります。工学や情報学は数学を応用して実際の問題を解いていく分野です。（でも、工学も情報学も、実は突き詰めると数学になってしまうことが多いのですけどね。）

図５の画像をどうやってコンピュータに分類させるか、というと、最近の工学や情報学では、沢山の学習用の「２」や他の数字の画像を用意してから、コンピュータに自動的に画像のどの辺を見ればよいか、そしてどのように分類をしたらいいか、判断させます。（沢山、というのはどれくらいか、というと、今回利用させてもらった「MNIST」という手書き数字のデータだと、学習画像に全部で6万枚、使われています。） 現在のこのやり方の正答率は、1万枚くらいのテスト画像で、世界一の性能で99.7～99.8%くらいになっています（1万枚で20～30枚しか間違えない）。私の共同研究者がちょっと試してみたところでも、99.1%くらいの正答率が出たそうです。今はこの分類の問題は簡単だと思われているので、もっと難しい分類や、なるべく少ないデータで汎用的な認識をするための研究が進んでいます。

私の毎日は、数学がいかに重要で、全ての基礎になっているかを実感する毎日、と言っても過言ではありません。ご紹介したベクトルや内積の考え方は、工学や情報学でも、（もちろん、他の分野でも）、幅広い応用の基礎になっています。研究分野で提案される手法は、数学的で汎用的であるほど、格調高いとされます。また、画像や文字の認識においては、「内積」に近い「畳み込み」という計算が常に利用されています。

このエッセイでは、数学、特に大学で習う線形代数の、ほんの一部を、画像を使って紹介しました。中学生でも大学生の数学が分かりそう、とか、「内積」って「積分」に似てるのかな、とか、「ベクトル」と「関数」って似ているのかな、とか、色々と感じた学生のみなさんは是非、もっと深く勉強してみてください。面白い発見に出会えると思います。 大丈夫です、私も数学が苦手でした。 今も苦手ですが、好きです。線形代数以外にも、数学は更に奥深く、面白く、便利な学問です。偉大な数学者たちに感謝し、どんどん活用する術を身に着けていきましょう。そして、数学の完璧さ、美しさ、素晴らしさ、をぜひ楽しみながら学んでいってください。

*1　三次元ベクトルは、たとえば、三次元の座標点もそうだし、ある時刻でのx方向、y方向、z方向の速度かもしれません。あるいは、「身長」「体重」「年齢」、あるいは、「国語」「算数」「英語」の成績、の数値を並べたものかもしれません。三つの量で表すものは、三次元のベクトルとして表せます。

*2　二次元や三次元の考え方を、より高次元、更には無限次元まで拡張したものをヒルベルト空間、と言います。名前は難しそうだけど、アイディアは分かりやすいですよね。

*3　ルールは何でもよく、縦に長いベクトルでもよいです。大事なことは、自分が興味を持って対象としている全ての画像が共通のやり方でベクトル化され、その後の数式の中でルールが記憶されていることです。

*4　画像の明るさを表すとき、２の乗数の範囲で表すのがコンピュータの中では便利です。ビット数と言ったりします。８ビット、つまり、２の８乗くらいあると、明るさをかなり綺麗に表現できます（最近のカメラだと２の12乗や２の16乗が使われたりもしています）。２の８乗=２５６の範囲で表そうとして、０から２５５までの数値を明るさとして割り当てています（255+1 = 256）。

*5　ベクトルの大きさについてもいくつか定義がありますが、まずはこの定義を理解していれば大丈夫です。

*6　aやbの大きさが $1$ より大きい時は、内積は $1$ より大きくなってしまうので、大きさを1にして考え直す必要があります。（注８も参考にしてください。）

*7　実数空間の内積の一つの定義です。実際に大学で数学を習うと、数学はこの他の内積の定義を許容してくれます。ですが、工学の分野だと、複素空間を扱うとき以外は、文中に書いた定義を内積と考えておいてよいと思います。数学は、もっと一般化した内積の定義をしてくれます。

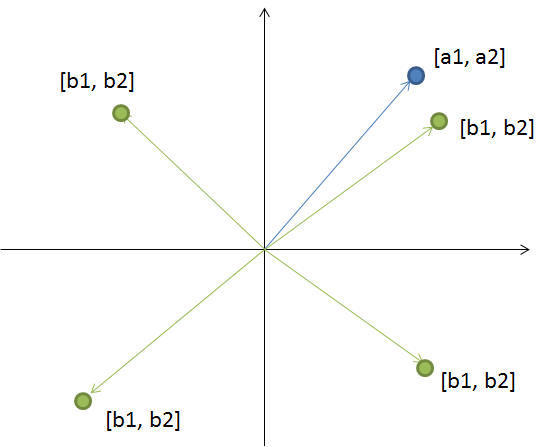
ちなみに、内積がなぜ要素同士の積の和でよいのか、2次元のベクトルを使って考えてみましょう。$[a_1,a_2]$というベクトルと、$[b_1, b_2]$というベクトルがあったとしますね。下の図のように、$[b_1, b_2]$の位置が色々と違う場合に、どうなるか考えてみましょう。$a_1$, $a_2$と$b_1$, $b_2$が全部正だったとき、要素同士の積の和である内積は大きくなりそうですね。逆に、$[a_1,a_2]$は第一象限にあるけれども、$[b_1, b_2]$は第二、あるいは第四象限にあるとき、内積は小さく、$0$に近くなりそうですね。$[b_1, b_2]$が第三象限にあるとき、内積は全体としては負になってしまいますが、絶対値自体は大きくなりそうです。内積が負、というのは、逆の方向を向いていることになり、大きさは、その方向が似ているかどうか、ということになります。要素同士の積の和で、ベクトルの向きが似ている、直交している、逆を向いている、などが表せることが理解できたでしょうか。次元が上がっても実は同じことが言えます。

*8　ベクトルの大きさを $1$ にすることを数学の言葉で「正規化」と呼んだりします。

[1] MNIST

※2016年12月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。