2次曲線の有理点
2次曲線
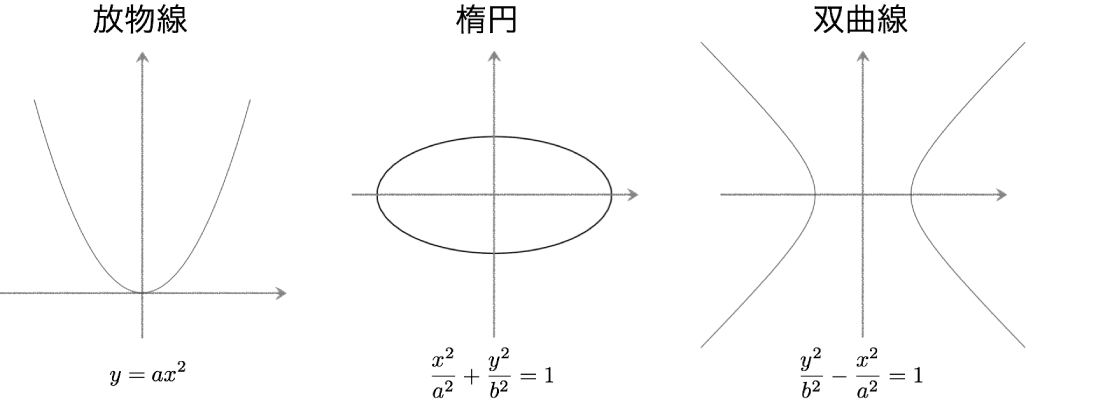
2次曲線とは一般的な方程式で $$ f (x,y) = a_1 x^2 + a_2 xy + a_3 y^2 + a_4 x + a_5 y + a_6 = 0, \qquad (a_1, \cdots, a_6 \in \mathbb{R}) $$ という形で表される曲線です。ただし退化している場合、すなわち、つまらないものになってしまう場合は除外しておきます。例えば $x^2-y^2=0$は$(x+y)(x-y)=0$となり、$2$つの直線 $x=y$, $x=-y$の合併になってしまうため除外しておきます。退化しない $2$次曲線を適当に変数変換すると、以下の3つの場合に帰着されることが知られています。
以下では2次曲線が$\mathbb{Q}$上定義された場合、すなわち $a$, $b$, $c \in \mathbb{Q}$の場合のみ考えます。2次曲線が扱いやすい理由は、パラメーター表示を持つからです。
2次曲線と有理点
有理数係数の2次曲線 $f(x,y)=0$ が与えられたとき、$f(x,y)=0$をみたす有理数の組$(x,y)$を、2次曲線 $f(x,y)=0$ の有理点と呼びます。 2次曲線の有理点は、パラメーターを用いることで、全て求めることができます。1つの例として、前節で紹介した円$x^2+y^2=1$の有理点を求める問題を考えてみましょう。
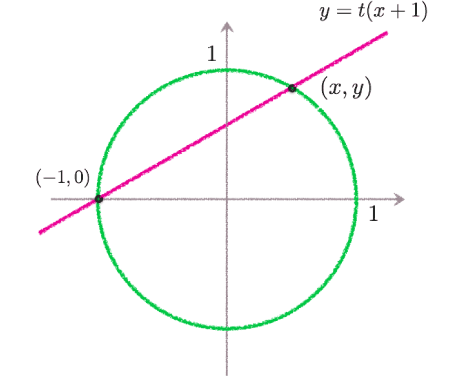
まず始めに点 $(-1,0)$は単位円上の有理点です。次にこの点を通り、傾きが$t$の直線 $ y = t(x+1) $ を考えます。この直線と単位円の交点を計算するために $$ \begin{cases} x^2+y^2 =1 \\ y=t(x+1) \end{cases} $$ を連立させると、 $(t^2+1) x^2 + 2t^2 x + t^2 – 1=0$となるので、$(-1,0)$と異なる直線と円の交点は $$ (x,y) = \left( \frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2} \right) $$ であることが分かります。
$t$ が有理数であれば、$(x,y)$も有理数となり、逆に交点$(x,y)$が有理数であれば、$(-1,0)$と$(x,y)$を結ぶ直線の傾きも有理数になります。また、直線 $x=-1$は点 $(-1,0)$で円と接するので、$x=-1$の傾きを便宜上 $t=\infty$と呼ぶことにすると、単位円$x^2+y^2=1$の有理点は、 $$ t \in \mathbb{Q} \cup \{ \infty \} $$ と1対1に対応していることが分かります。 $\mathbb{Q} \cup \{ \infty \}$は射影直線と呼ばれ、$\mathbb{P}^1(\mathbb{Q})$などと記されます。すなわち単位円$x^2+y^2=1$の点は、射影直線$\mathbb{P}^1(\mathbb{Q})$の点と1対1に対応することが導かれました。
双曲線でも似たようなことができます。
問題 双曲線 $x^2 – y^2 = 3$ の有理点を求めよ。
上の問題では、2つの漸近線のかなたに無限点があるとして下さい。そうするとこの場合でも、2つの無限遠点を含めた有理点の集合は$\mathbb{P}^1(\mathbb{Q})$の点と1対1に対応することが導かれます。
2次曲線に有理点が1つでも存在すれば、以上の方法で、その2次曲線の無限点も含めた有理点全体の集合は$\mathbb{P}^1(\mathbb{Q})$の点と1対1に対応していることが分かります。それでは、2次曲線には必ず有理点が少なくとも1つは存在するのでしょうか?
有理点が無い場合
実平面の中には有理点がびっしりと詰まっているので、有理点を避けて通る曲線なんて無いような気がしてしまうかもしれません。しかし、有理点を持たない2次曲線も、実はいっぱい存在するのです。例えば、次の結果が知られています。
命題 $x^2+y^2=3$をみたす有理数 $x,y\in\mathbb{Q}$は存在しない。
【証明】背理法で証明します。有理数解 $x,y$ が存在すると仮定します。通分すると、$x=X/Z$、$y= Y/Z$、ただし $X,Y,Z\in\mathbb{Z}$と書けます。方程式は $X^2+Y^2=3Z^2$となります。$X$, $Y$, $Z$の最大公約数を $d$ としたとき、$X’=X/d$, $Y’=Y/d$, $Z’=Z/d$とおいて$X,Y,Z$のかわりに用いることで、$X,Y,Z$の最大公約数は$1$であると仮定できます。整数 $m$を3で割った時のあまりを$m\pmod{3}$と書き、整数$m$と$n$を3で割った時のあまりが一致するときに$m \equiv n \pmod{3}$と書くことにします。この記号を使うと $$ X^2 + Y^2 \equiv 0 \pmod{3} $$ となります。$X,Y\equiv 0,1,2 \pmod{3}$に対して、$X^2\equiv 0,1 \pmod{3}$, $Y^2\equiv 0,1 \pmod{3}$となります。従って、上の方程式をみたすのは、$X^2\equiv Y^2\equiv0 \pmod{3}$、すなわち$X\equiv Y\equiv0 \pmod{3}$ のときだけとなります。このことは、$X$と$Y$が $3$ の倍数であることを意味し、方程式から $Z$も$3$の倍数となってしまいます。これは$X$, $Y$, $Z$ の最大公約数が $1$ であることに矛盾しています。従って、有理数解$x$, $y$ は存在しないことが導かれます。$\square$
平面に半径 $3$の単位円を書いてみて下さい。上の結果から、この円上のどの点をとっても、それは有理点でないことが分かります。平面上にびっしりと有理点があるにも関わらず、この円は、なぜか有理点をうまく避けています。
問題 $x^2 – 2 y^2 = 3$をみたす有理数 $x,y\in\mathbb{Q}$は存在するか?
以上のことから、2次曲線の無限遠点を含めた有理点の集合は、$\mathbb{P}^1(\mathbb{Q})$か空集合かのいずれかになることが分かります。
※2016年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。