複素数のかけ算

極座標表示

$i = \sqrt{-1}$として複素数$\alpha = a + i b$が与えられたとき、この数を平面上の点$(a,b)$と対応させることで、複素数と実数平面の点を対応させることができます。この様に複素数を平面上の点として幾何学的に見ると、複素数のかけ算も幾何学的に解釈することが可能となります。

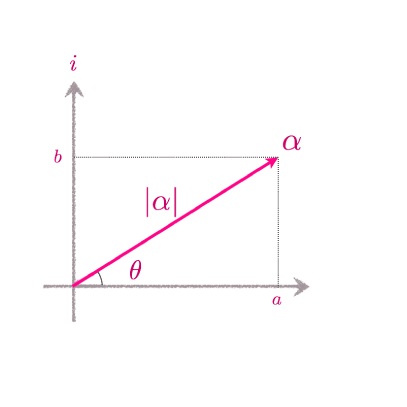
複素数$\alpha = a + ib$が与えられた時、$\alpha$と原点を結ぶ線分が実軸となす角度を$\alpha$の偏角と呼び、$\arg(\alpha)$と記します。また、$\alpha$と原点の距離$\sqrt{a^2+b^2}$を$\alpha$の絶対値と呼び、$|\alpha|$と記します。$\theta = \arg(\alpha)$と置くと、$\cos\theta = a / |\alpha|$, $\sin\theta = b/|\alpha|$となることから、 $$ \alpha = a + i b = |\alpha| \biggl(\frac{a}{|\alpha|} + i\frac{b}{|\alpha|}\biggr) = |\alpha| (\cos \theta + i \sin \theta) $$ と表されます。この表示を複素数の極座標表示と呼びます。

かけ算と極座標表示

複素数 $\alpha = a + i b$と$\beta = c + i d$の積を計算すると、 $$ \alpha \beta = (a + ib)(c + id) = (ac – bd) + i (ad+bc) $$ となります。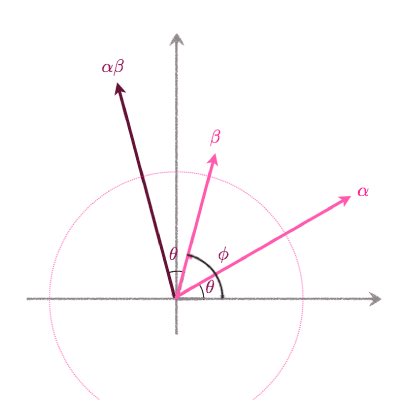 03_21_02 $\theta = \arg(\alpha)$, $\phi = \arg(\beta)$と置いて、このかけ算を極座標表示 \begin{align} \alpha &= |\alpha| (\cos \theta + i \sin \theta) & \beta &= |\beta| (\cos \phi + i \sin \phi) \end{align} で表すと、 \begin{align} \alpha\beta &= (|\alpha| (\cos \theta + i \sin \theta ))(|\beta|( \cos \phi + i \sin \phi))\\ &= |\alpha||\beta| ((\cos \theta \cos \phi – \sin \theta \sin \phi) + i (\cos \theta \sin \phi + \sin \theta \cos \phi))\\ &= |\alpha||\beta|( \cos(\theta+\phi) + i \sin(\theta + \phi)) \end{align} となります。最後の等号は、$\cos$と$\sin$の和の公式のよって導かれます。従って、複素数のかけ算は、２つの複素数の絶対値を掛け合わせて、偏角を足したものになります。この様に、一見複雑そうな複素数のかけ算も、幾何学的な見方をすると、より見やすい意味を持つことが分かります。

$1$ の $3$ 乗根

この見方を利用すると、$\omega = \frac{-1+\sqrt{-3}}{2}$に対して、$|\omega|=1$で $$ \omega = \frac{-1+\sqrt{-3}}{2} = \cos(2\pi/3) + i \sin(2 \pi/3) $$ であることに注意すると、 \begin{align} \omega^2 &= \cos(4\pi/3) + i \sin(4 \pi/3) = \frac{-1-\sqrt{-3}}{2} \\ \omega^3 &= \cos(6\pi/3) + i \sin(6 \pi/3) =1 \\ \end{align} となることが計算できます。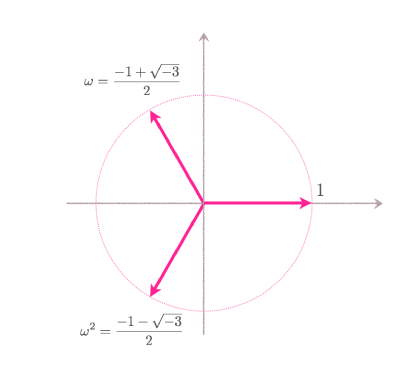 03_21_03 従って、$\omega$ は$3$乗すると$1$になることが分かります。このことから、$\omega$ は$1$の$3$乗根であると言います。

これは、$f(X) = X^3-1$と置くと、$\omega$ は $f(X)=0$の解であることを意味します。$f(X) = (X-1)(X^2+X+1)$と因数分解でき、$\omega-1 \neq 0$であることから、 $$ \omega^2+\omega+1=0 $$ が成り立つことも従います。

$1$ の $n$ 乗根

より一般に、自然数 $n=1,2,\cdots$に対して $$ \zeta_n = \cos(2\pi/n) + i \sin(2 \pi/n) $$ と置くと、$\zeta_n$は$n$乗すると$1$になる複素数であることが分かります。このことから、$\zeta_n$は$1$の$n$乗根であると言います。 $\omega$の場合と同様に、$\zeta_n$は　$f_n(X) = X^n-1$に対して　$f_n(X)=0$ の解であり、$f_n(X) = (X-1)(X^{n-1} + X^{n-2} + \cdots + X+1)$と因数分解できることから $$ \zeta_n^{n-1} + \zeta_n^{n-2} + \cdots + \zeta_n + 1 = 0 $$ が成り立つことも確かめられます。