結び目理論から生まれたゲーム「領域選択ゲーム」
1.結び目理論とは
ひもを適当に絡ませて、両端をつなげてみましょう。これが結び目理論でいう「結び目」です。

結び目理論では結び目の絡まり方を数学的に研究します。結び目理論は数学や数学以外の色々な分野とのつながりも深く、幅広く応用されている分野でもあります。
2.領域選択ゲーム
ここでは、結び目理論の研究から生まれた「領域選択ゲーム」というゲームを紹介します。結び目射影図とは、結び目を平面や球面にうつした影のことです。ただし交点は2重点のみで、横断的に交わるものとします。つまり、各交点を直進して一筆書きで描ける閉じた曲線のことです。結び目射影図の線で囲まれたそれぞれの部分を領域といいます。余談ですが、球面上の結び目射影図において、「(領域の数)=(交点の数)+2」が常に成り立ちます。例えば下の図において、領域の数は8、交点の数は6となり関係式が成り立っていますね。気になる人はぜひ「オイラー標数」についても調べてみてくださいね!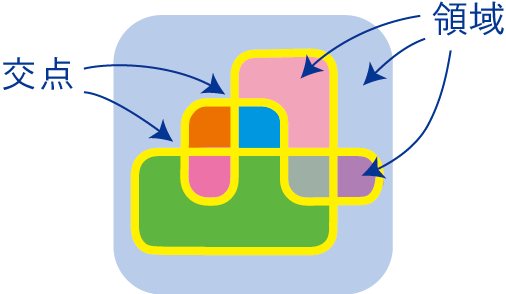 さて、結び目射影図の各交点に、オン/オフが切り替えられるランプを置きます。領域選択ゲームは次のようなゲームです。ランプ付き結び目射影図の領域を選択すると、その境界上にあるランプのオン/オフが一斉に切り替わります。領域を選択していき、全てのランプを点灯できたらゲーム終了です。
さて、結び目射影図の各交点に、オン/オフが切り替えられるランプを置きます。領域選択ゲームは次のようなゲームです。ランプ付き結び目射影図の領域を選択すると、その境界上にあるランプのオン/オフが一斉に切り替わります。領域を選択していき、全てのランプを点灯できたらゲーム終了です。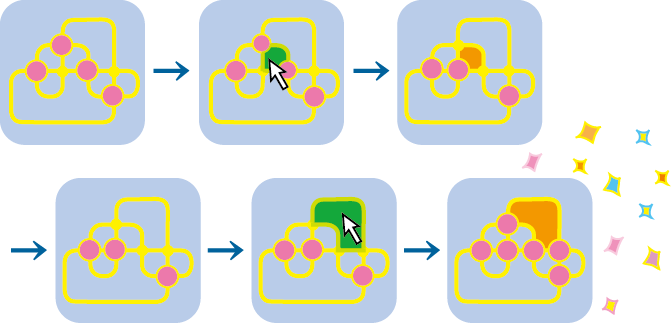
大阪市立大学数学研究所のホームページ上で領域選択ゲームで遊ぶことができます。また、Androidのアプリにもなっています。このゲームは、どんな結び目射影図でも、どんなランプの初期状態でも、必ずクリアできるということが結び目理論のある研究結果 (領域交差交換という変形に関する研究です) を用いて証明できます。
3.領域選択ゲームの攻略法
領域選択ゲームは、 他のゲームやパズルと同様にたくさん遊べば遊ぶほど慣れて上手に早くクリアできるようになりますが、攻略法を用いて遊ぶのも楽しいものです。また、新しい攻略法を見つけるのも楽しいですね。ここでは図形的な攻略法をひとつ紹介します。
ある結び目射影図をこれからPと呼びましょう。(ここでは簡単のため、“既約な射影図”というもののみを考えます。) Pのある交点をcと呼びましょう。これから、cのランプだけを変えるような、Pの領域たちの見つけ方を3ステップで紹介します。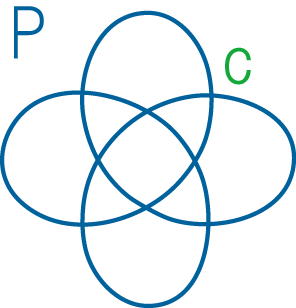
ステップ1:Pに向きをつけて c でスプライスする。
まずPに、各交点を直進して一方通行になるような向きを与えます。結び目射影図には2通りの向きの与え方がありますが、好きな方でOKです。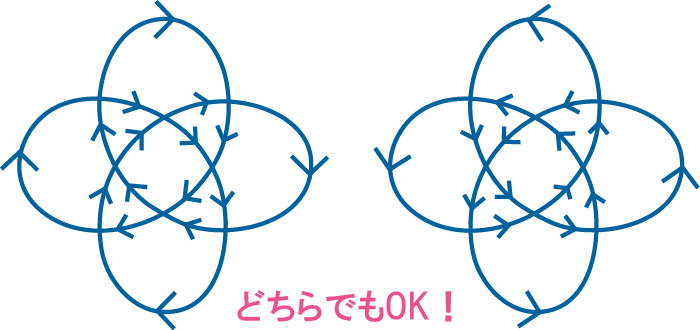
交点cにおいて「スプライス」とよばれる操作を行います。交点cでのスプライスとは、向きを保ったまま交点cをなくすように結び目射影図をつなぎかえる操作のことです。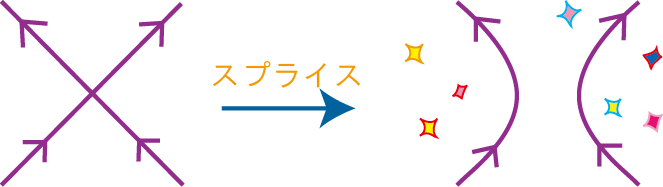
結び目射影図を1回スプライスすると、2つの結び目の射影図になります。(スプライスする交点のまわりのつながり方を考えることで確認できます。)
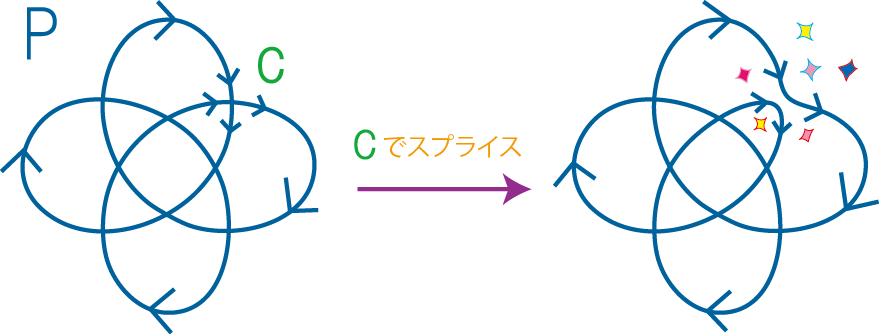
これらをP1、 P2と呼びましょう。スプライスが終わったら、射影図の向きのことは忘れてしまいましょう!
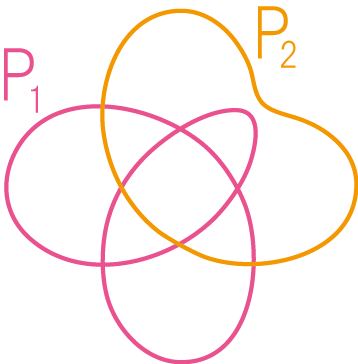 ステップ2:片方の結び目射影図をチェッカーボード彩色する。
ステップ2:片方の結び目射影図をチェッカーボード彩色する。
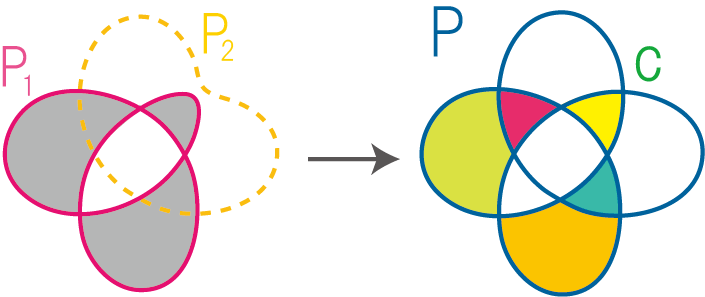
ステップ1で得られた2つの結び目射影図のうちの片方、例えばP1に対して「チェッカーボード彩色」とよばれる、領域の塗り分けをします。チェッカーボード彩色とは結び目射影図の各領域を、隣り合う領域が異なる色となるように白と黒の2色 (もちろんピンクと水色、とか2色なら何でもOKです!) で塗り分ける彩色のことです。任意の結び目射影図に対して、必ずチェッカーボード彩色を与えることができます。(気になる人は理由を考えてみてくださいね!)

それではP1をチェッカーボード彩色しましょう。ただし、P2のことは今だけ忘れて、P1だけを見ます。
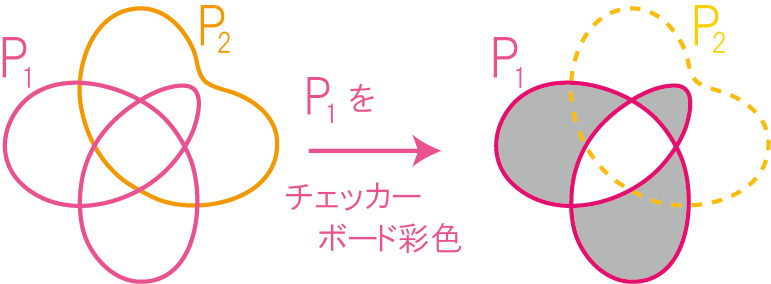
ステップ3:黒領域に対応するPの領域を見る。
ステップ2では、 P1をチェッカーボード彩色しました。そこで黒色に塗った領域に対応するPの領域たちは、次の条件を満たしています。
・P1どうしの交点に対応するPの交点のまわりには2領域ある。
・P2どうしの交点に対応するPの交点のまわりには0領域、または4領域ある。
・P1とP2の交点に対応するPの交点のまわりには2領域ある。
・交点cの周りには1領域または3領域ある。
まとめるとこの領域たちは、交点cのまわりには奇数個でそれ以外の全ての交点のまわりにはそれぞれ偶数個ある、ということになります。これが、求めたかった領域たちとなります。つまりこの領域たちを、好きな順番で1回ずつ選択すると、交点cのランプの状態だけが変わるのです。
このアルゴリズムを繰り返すことによって、全てのランプを点灯させることができるのです!この他にも、連立方程式による攻略法や、結び目射影図ごとの攻略法など色々な攻略法があるので、ぜひ考えてみてくださいね。
4.領域選択ゲームの活躍
領域選択ゲームは今、様々な方面に応用され始めています。数字や文字を使わず直感的に楽しめる数学ゲームなので、図形に早くから親しむことや数手先を読む力の向上を期待して幼児教育への応用の研究がされています。

また空間認識力の向上なども期待して、リハビリへの応用の取り組みもなされています。
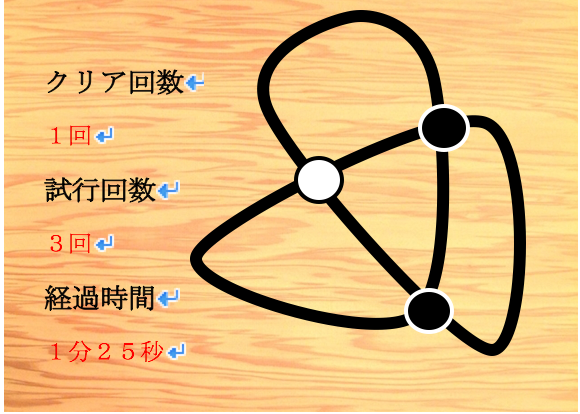
さらに、結び目の領域と交点の関係を利用したスイッチへの応用なども考えられています。

*この原稿を執筆してくださった清水理佳先生は 数理女子のリアルライフにも「高専教員数理女子のリアルライフ」という記事をご寄稿くださってます。
※2016年9月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。


