博士論文とは、大学卒業後、大学院の修士課程を修了し、さらに博士課程へ進んで研究した内容をまとめたものです。難しい言葉もたくさんあります。わからないことだらけでも全く大丈夫！！研究の雰囲気や、数学の世界にどんな分野やテーマがあるのか感じてもらえればと思います。研究者同士でも、お互いの博士論文の内容はなかなか理解できるものではありません。実はわからないことって面白いことの始まりです。存分に楽しんでください♪

論文題目「Richard Thompson’s groups from the viewpoint of geometric group theory」
(　東京大学にて取得。)

1　研究分野：幾何学的群論

　私の研究分野は幾何学的群論で、研究の対象はある群^*1です。まず研究分野について紹介するために、M. Bridsonによるサーベイ論文^*2を紹介したいと思います。この論文の「Figure 1」の一部を書き写したものが、次の図です。

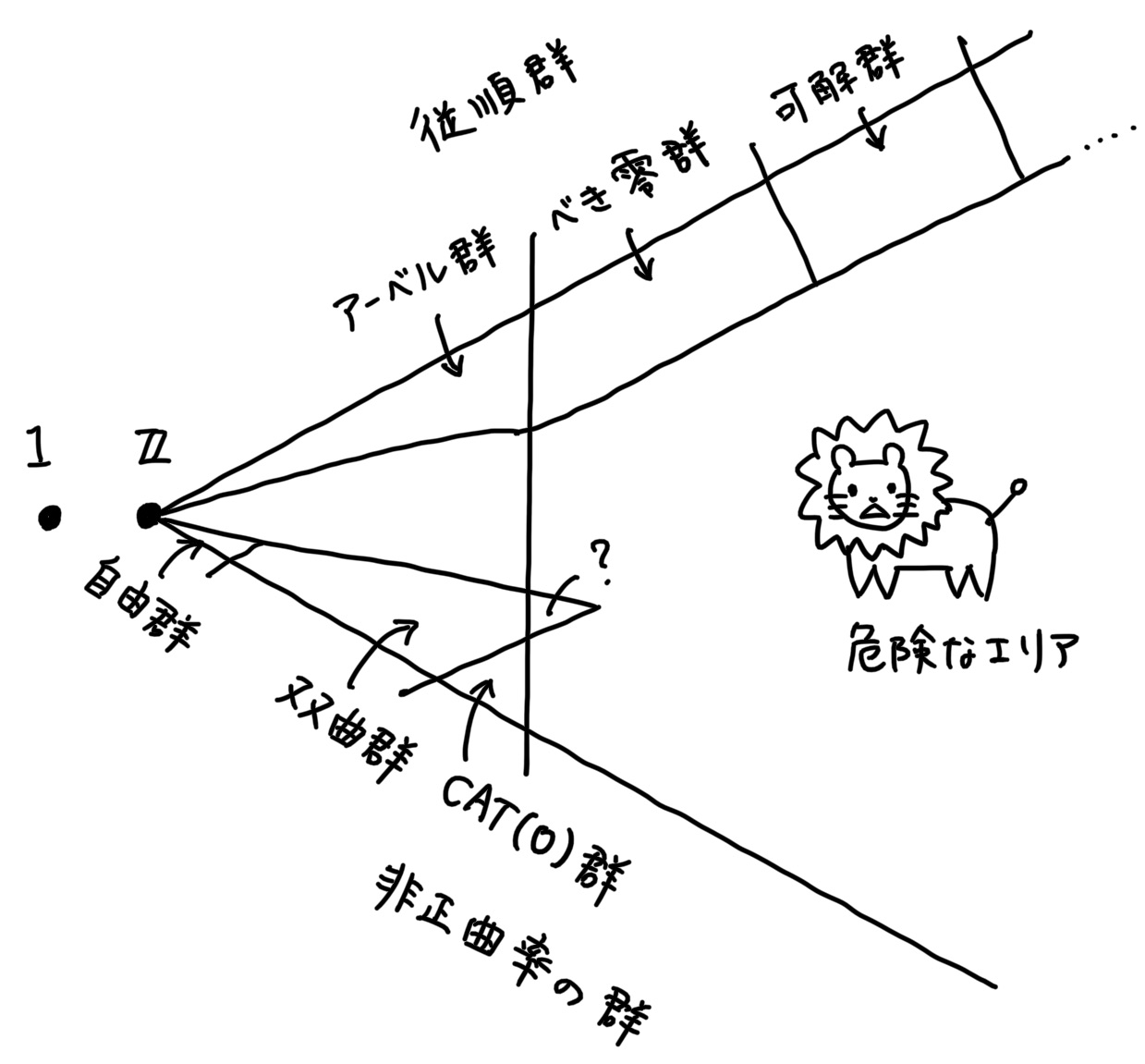
　この図は、群の生息する世界の地図を表していて、様々な群の生息域が示されています（群の名前に馴染みがない方は、「いろんな生物がいるように、群にもいろいろあるんだな」くらいにとらえてください）。たとえば、有限群は、地図上のある島に描かれていますが、大域的な図なので、島は1点に見えます。以下では有限群は無視して、無限群を調べることを考えます。無限群は大陸に分布しています。大陸を探検するルートは主に二つあります。一つ目は、「従順群」の生息域をたどるルートです。このルートを辿っていくと、可換群やべき零群や可解群に出会えます。もう一つは、「非正曲率の群」の生息域をたどるルートです。このルートに沿って進むと、まず自由群に出会えて、そのうちグロモフの双曲群やCAT(0)群なども出てきます。第一のルートと第二のルートは、起点は同じ群（ℤ）ですが、方向は別々です。ルートを外れると、それまでの勘や経験が通用せず、危険に遭うこともあります(ライオン^*3)。

2　研究対象：Thompson群

　 私が興味を持っている群は、Thompson群と呼ばれる群です。Thompson群には何種類かあるのですが、代表的なものであるThompson群Fについて、二種類の定義を紹介します。

定義2.1．集合Fを、全単射写像f:[0,1]→[0,1]のうち、次の条件を満たすものの集合とする：

   1. 区分的に線型（すなわち、折れ線グラフで表される写像）。
　2. a/(2^b)（a, bは自然数）と表される有限個の点を除いて微分可能（折れ線グラフの折れている点は有限個で、そのx座標はa/(2^b)のように表せる）。
　3. 微分可能な点での傾きは2^k（k∈ℤ）。

このとき、Fは写像の合成を演算として群をなす。これをThompson群Fとよぶ。

　例えば、次のような写像はFの元の例です。

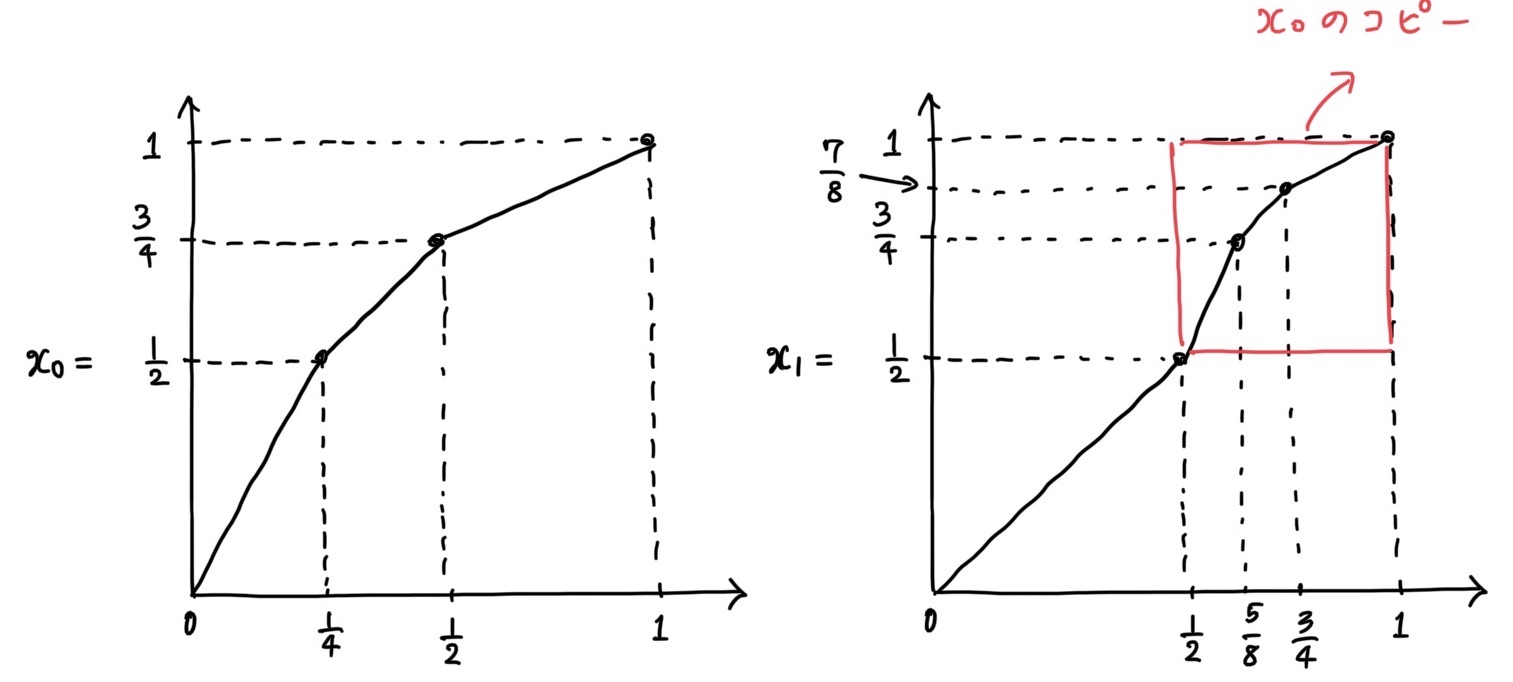
　$x$₀, $x$₁は位数無限なので、Fが無限群であることがわかります。また、$x$₀, $x$₁は非可換であることから、Fが非可換群であることもわかります。

定義2.2.　次の群表示で定義される群をThompson群Fとよぶ:

　定義2.2の群表示は、有限表示に取り換えることができます（すなわち、Fは有限表示群）。また、図2の$x$₁のように「$x$₀の1/2ⁿスケールの縮小コピー」として定義される元を$x$_nとおくと、$x$₀, $x$₁, . . . $x$_n . . .は定義2.2の表示の関係式を満たすことが確認できます。これによって定義2.1の群から定義2.2の群への準同型写像が得られますが、この写像は同型になることが証明できます。
　FがBridsonの地図上でどの辺にいる（べき）かはよくわかっていません。実際、「Fが従順群（つまり、地図で第一のルート上にいる群）である」という予想は大きな未解決問題です。正しそうか正しくなさそうかも、人によって意見がバラバラで、ZFC公理系から独立なのではないかという説さえあるそうです。せめて方向性が見えていたらいいのになあ、と思いますが、正体がつかみづらい点も魅力かもしれません。

３　私の博士論文

　私の博士論文の研究は、Thompson群のCAT(0)空間への作用にはどの程度良いものがあるか、ということをテーマにしています。「研究分野について」での表現を使うと、Bridsonの地図上で、Thompson群の生息域が第二の探索ルートとどの程度近いか、という問題意識と言えます。　　　
　この研究では、Thompson群Fだけでなく、その「S¹版」である群Tと、「カントール集合版」である群V、およびそれらの一般化に注目しました。 Farleyの結果により、F, T, Vとその一般化は無限次元のCAT(0)立方複体に固有かつ等長に作用していることが知られていました^*4。また、1次元CAT(0)立方複体(=木)の場合には、T, Vの作用で固有かつ等長なものは存在しない（より強く、等長な作用は固定点を持つ）ことが知られていました^*5。このように、1次元と無限次元の場合の結果が知られていたため、その間の有限次元の場合がどうなっているかに興味を持って研究を行いました。
　結果として、有限次元の場合は1次元の場合と同じ状況（すなわち、有限次元CAT(0)立方複体への等長作用は固定点を持つ）ことを示すことができました^*6。この結果により、「任意の有限次元のCAT(0)立方複体への等長作用は固定点を持つ」という性質を持つが、「無限次元のCAT(0)立方複体への群作用への等長作用は固定点を持つ」という性質を持たない群があることもわかりました。

４　展望

　今回の文章では、従順性との関連でThompson群を紹介しましたが、この群はもっと様々な研究領域に関係して現れます。その例を三つ紹介します。

・数論との関係。Thompson群Fの定義で、2のかわりにn（n∈ℕ_≥３）を考えると、別の群F$n$を定義することができます。これをHigman-Thompson群またはBrown-Thompson群と呼びます。また、いくつかの自然数 $n_1,\ldots,n_l$を同時に用いて、別の群F($n_1,\ldots,n_l$ )を考えることもできます。これをStein-Thompson群と呼びます。F$n$やF($n_1,\ldots,n_l$)の性質は、nや$n_1,\ldots,n_l$の取り方に応じて違いが出ることが知られており、数論的な条件付けが現れます。

・結び目理論との関係。Jonesは、Thompson群の元に絡み目を対応させる方法を考えました（図3）。この対応は1:1ではありませんが、全ての絡み目を作ることができます^*7。

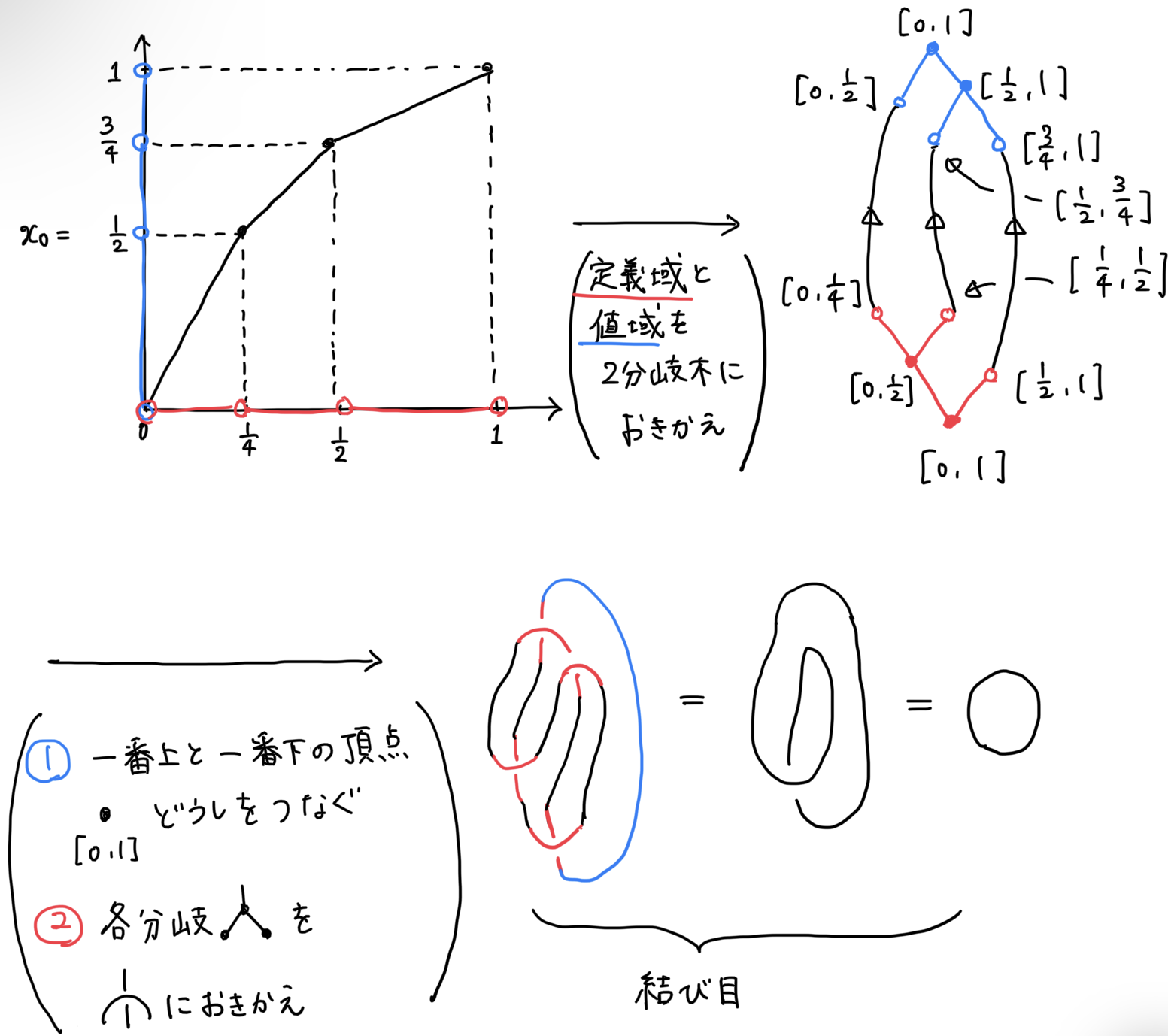
・暗号理論への応用。Shpilrain とUshakovは、Thompson群を利用した公開鍵暗号を提案しました^*8。その後攻撃方法が見つかっていますが、Thompson群の様々な一般化についても、暗号への応用が研究されています。

現在は、上記のような、博士論文の問題意識とはやや離れたトピックにも興味を持っています。
今後もまた、今まで予想しなかった方向に進んでいくかもしれません。分野の近い方はもちろん、全く違う分野の方も、今後お話する機会があればぜひよろしくお願いします。

*1 この原稿で出てくる群はすべて有限表示群です。

*2 M.Bridson,Non-positive curvature and complexity for finitely presented groups, International Congress of Mathematicians. Vol. II, 961-987, Eur. Math. Soc., Zürich, 2006.

*3 元の図にもちゃんといます。

*4 D.S. Farley, Actions of Picture Groups on CAT(0) Cubical Complexes. Geom. 110， 221-242 (2005)

*5 D.S. Farley, A proof that Thompson’s groups have infinitely many relative ends.　 J. Group Theory 14 (2011), no. 5, 649-656.

*6 同じ結果がGenevois(A. Genevois, Hyperbolic and cubical rigidities of Thompson’s group V. J. Group Theory 22 (2019), no.2, 313-345. )によってより早く発表されています。証明手法は異なり、私の手法はGenevoisの手法（CAT(0)立方複体の幾何学を使う）と比べて初等的ですが、立方複体でない場合も扱えるため、空間に対する条件を弱めることができます。

*7 V. F. R. Jones, Some unitary representations of Thompson’s groups F and T.  J. Comb. Algebra 1(2017), no. 1, 1-44.

*8 V. Shpilrain and A. Ushakov, A new key exchange protocol based on the decomposition problem.　Al-gebraic methods in cryptography, 161-167, Contemp.Math., 418, Amer. Math. Soc., Providence, RI, 2006.

※2023年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。